Roots of polynomial equations II

This page is the second of a two-part series on polynomial root-finding methods. For a background on Newton’s method as well as Halley’s and the Secant method, see part I.

Periodic attractor basins

Let’s look closer at the areas that converge slowly for Newton’s method applied to the equation $z^5-z-1$. A little experimentation suggests that these areas may never converge on a root, as increasing the maximum iteration number for Newton’s method fails to change them. Tracking iterations that start in the central (near the origin, that is) sowly-converging area, many are found to converge on the period-3 orbit

\[-1.000257..., -0.750321..., 0.0833570..., -1.000257...\]

Certainly there are some points in the plane, such as $\pm \sqrt[4]{1/5}$, which do not converge on anything at all. But do the other starting points in the slowly-converging region eventually end up in this periodic orbit? This can be tested for each point plotted for Newton’s method (code for this section here) After 80 iterations, nearly all points head towards a root or else to the periodic orbit above:

What about the non-converging areas on the periphery? If we follow the trajectory from the point $4.707 - 4.117i$,

the outer region is mapped to the inner region. This is also appears to the the case for initial points far from the origin that do end up converging on a root. Such observations suggest that initial points far from the origin may stay arbitrarily close together until entering the central region. Is this the true for the points plotted previously?

This can be tested by checking how long it takes for two arrays shifted by a small amount (here 0.0000001) to come near each other:

def traveling_together(equation, max_iterations, x_range, y_range):
	"""
	Returns points that stay near points nearby in future iteration.

	Args:
		equation: str, polynomial of interest
		max_iterations: int of iterations
		x_range: int, number of real values per output
		y_range: int, number of imaginary values per output

	Returns:
		iterations_until_together: np.arr[int] (2D) 
		
	"""

	y, x = np.ogrid[2: -2: y_range*1j, -2: 2: x_range*1j]
	z_array = x + y*1j
	z_array_2 = z_array + 0.0000001 # arbitrary change, can be any small amount
	iterations_until_together = max_iterations + np.zeros(z_array.shape)

	# create a boolean table of all 'true'
	not_already_together = iterations_until_together < 10000

	# initialize calculate objects
	nondiff = Calculate(equation, differentiate=False)
	diffed = Calculate(equation, differentiate=True)

	for i in range(max_iterations):
		f_now = nondiff.evaluate(z_array) 
		f_prime_now = diffed.evaluate(z_array)
		z_array = z_array - f_now / f_prime_now

		f_2_now = nondiff.evaluate(z_array_2) 
		f_2_prime_now = diffed.evaluate(z_array_2)		
		z_array_2 = z_array_2 - f_2_now / f_2_prime_now

		# the boolean map is tested for rooted values
		together = (abs(z_array - z_array_2) <= 0.0000001) & not_already_together
		iterations_until_together[together] = i
		not_already_together = np.invert(together) & not_already_together

	return iterations_until_together

which yields

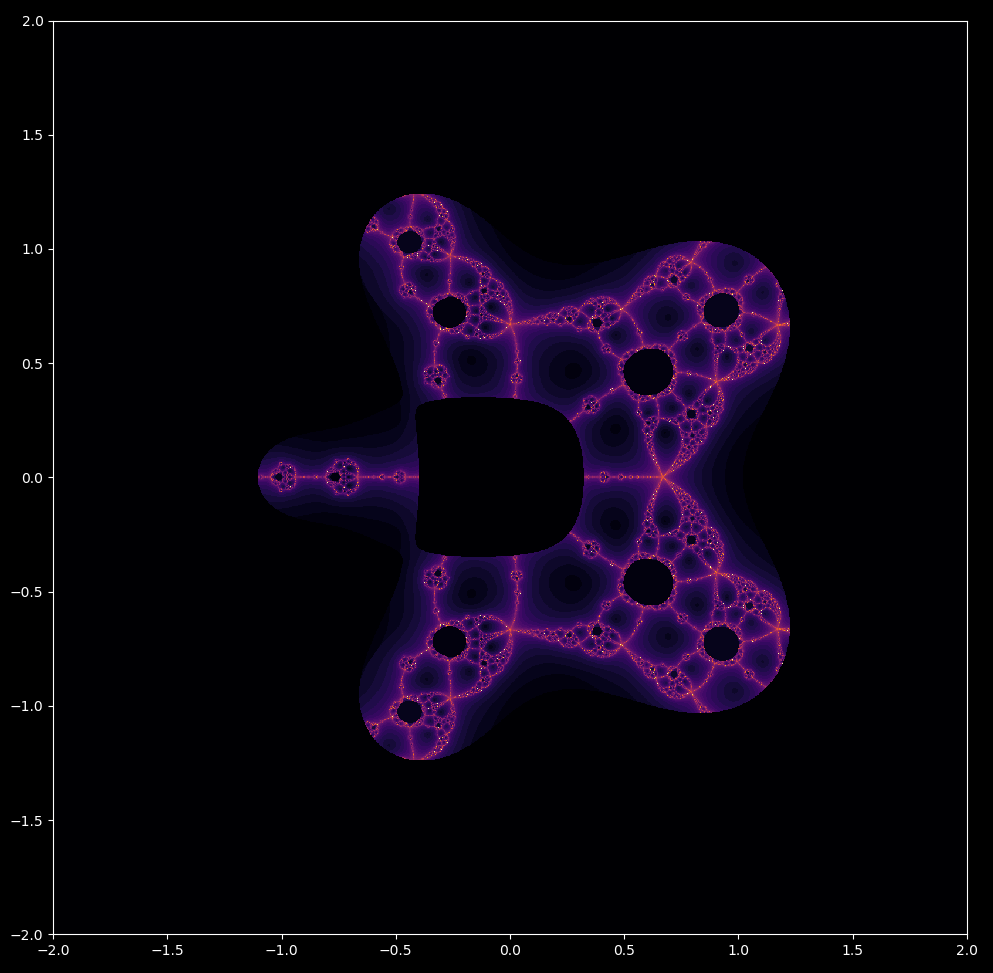
All mapped points outside a certain radius from the origin stay near each other for their first iteration. This is also the case for $z^3-1$,

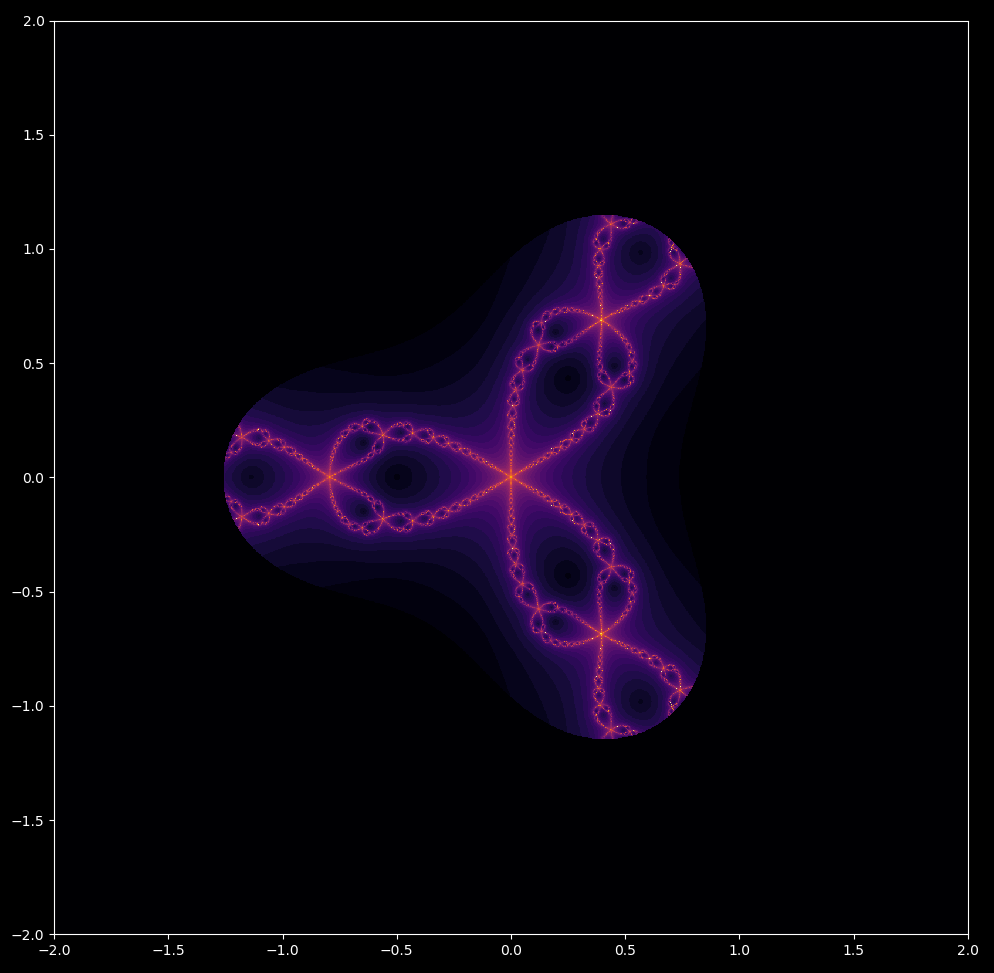
And for incremental powers between $z^1-z-1$ and $z^6-z-1$

Julia and Mandelbrot sets in Newton’s map

Let’s look closer at the periodic attractor in Newton’s map of $z^5-z-1$

A keen-eyed observer may note that this region resembles a slightly squashed (and filled-in) Julia set defined by

\[z_{n+1} = z_n^2 + (0.5 + 0i)\]

which when mapped in the complex plane appears as

In the case of this Newton map, we are observing initial points in the complex plane that either do or do not converge on a root whereas for classically defined Julia sets, we are interested in initial points in the complex plane that either diverge to infinity or else end up in a periodic orbit. Thus by assigning points that find roots using Newton’s method to be equivalent to points that head towards infinity, we arrive at the interesting conclusion that these Newton fractals are analagous to Julia sets, broadly defined.

Where there are Julia sets, one can often find a Mandelbrot set. This means that Julia sets are defined by fixing a dynamical equation and observing which initial points in the complex plane diverge or are trapped in periodic trajectories, and the generalized Mandelbrot set is defined by allowing the equation to change according to various points in the complex plane whilst holding the intial point constant at the origin.

Similarly, we can see which points find a root (ie which head to ‘infinity’) given a starting value of $0 + 0i$ and an addition of the given point to Newton’s map. In symbols, we are interested in the map

\[z_{n+1} = z_{n} + \frac{f(z)}{f'(z)} + a \\ z_0 = 0 + 0i \\ a \in \Bbb C\]

which can be observed using the following code:

def newton_boundary(equation, max_iterations, x_range, y_range):
	...
	y, x = np.ogrid[0.045: -0.045: y_range*1j, -0.045: 0.045: x_range*1j]
	a_array = x + y*1j
	z_array = np.zeros(a_array.shape)

	iterations_until_rooted = np.zeros(z_array.shape)

	 # create a boolean grid of all 'true'
	not_already_at_root = iterations_until_rooted < 10000

	nondiff = Calculate(equation, differentiate=False)
	diffed = Calculate(equation, differentiate=True)

	for i in range(max_iterations):
		iterations_until_rooted[not_already_at_root] = i
		previous_z_array = z_array
		z = z_array
		f_now = nondiff.evaluate(z)
		f_prime_now = diffed.evaluate(z)
		z_array = z_array - f_now / f_prime_now + a_array

		# the boolean map is tested for rooted values
		found_root = (abs(z_array - previous_z_array) < 0.0000001) & not_already_at_root
		iterations_until_rooted[found_root] = i
		not_already_at_root = np.invert(found_root) & not_already_at_root

	return iterations_until_rooted

Looking close to the origin, we find a (slightly distorted) Mandelbrot set has replaced our Julia set.

More accurately, this is actually a mix of Mandelbrot

\[z_{n+1} = z_{n}^2 + a \\\]

and what is sometimes called Multibrot

\[z_{n+1} = z_{n}^b + a \\ b > 2\]

sets, which is perhaps not altogether surprising being that our polynomial of interest is a fifth degree entity and thus encompasses both second and fourth dergree polynomials. Zooming in by a factor of $10^7$ on one of these fourth-degree Multibrots, we have

A true mandelbrot set may be found by proceeding with the same interation procedure described above for the equation

\[z^3 - z - 1\]

when increasing scale by $10^7$ at the point

\[0.19379287 + 0.002549i\]

we have (note that the Mandelbrot set interior fails to converge as for the multibrot above but the color was changed to highlight the border for visual flair)

Incrementing powers

Maps of convergence using Newton’s method display sensitivity to initial conditions: points arbitrarily nearby to each other in the complex plane may have very different times to convergence. In addition, the exponential powers of the input equation displays analagous behavior: small changes in exponent magnitude lead to large changes for which starting points find roots quickly. As $a$ is increased past 1, $z^5-z^{a}-1$ yields (right click to view in higher resolution)

Upon incrementing $z^5-z-1 \to z^5-z^{1.033}-1$,

For the equation

\[z^7-z-1\]

with roots estimated via Newton’s method (centered on the origin), we have

at $z^{7.11}-z-1$,

and at $z^{7.14}-z-1$

From $z^7-z-1$ to $z^{7.397}-z-1$,

and from $z^7-z-1$ to $z^{7.1438555}-z-1$, incremented slowly,

In the last section, we observed some polynomials with complex values,meaning that instead of focusing on real constants and exponents and allowing the unkown to assume complex values, now $a_n, b_n \in \Bbb C$ for polynomials

\[a_0x^{b_0} + a_1x^{b_1} + a_2x^{b_2} + \cdots\]

The results for

\[z^{5 + 0i}-z-1 \to \\ z^{5 + 0.2802i}-z-1\]

are as follows:

and for a longer video of

\[z^{7.11}-z-1 \to \\ z^{7.11 + 0.002271i}-z^{1+0.002271i}-1\]

we have