Dynamics
The mathematical approach to change over time. Most dynamical systems are nonlinear and generally unsolvable, and though deterministic are often unpredictable.
Logistic map
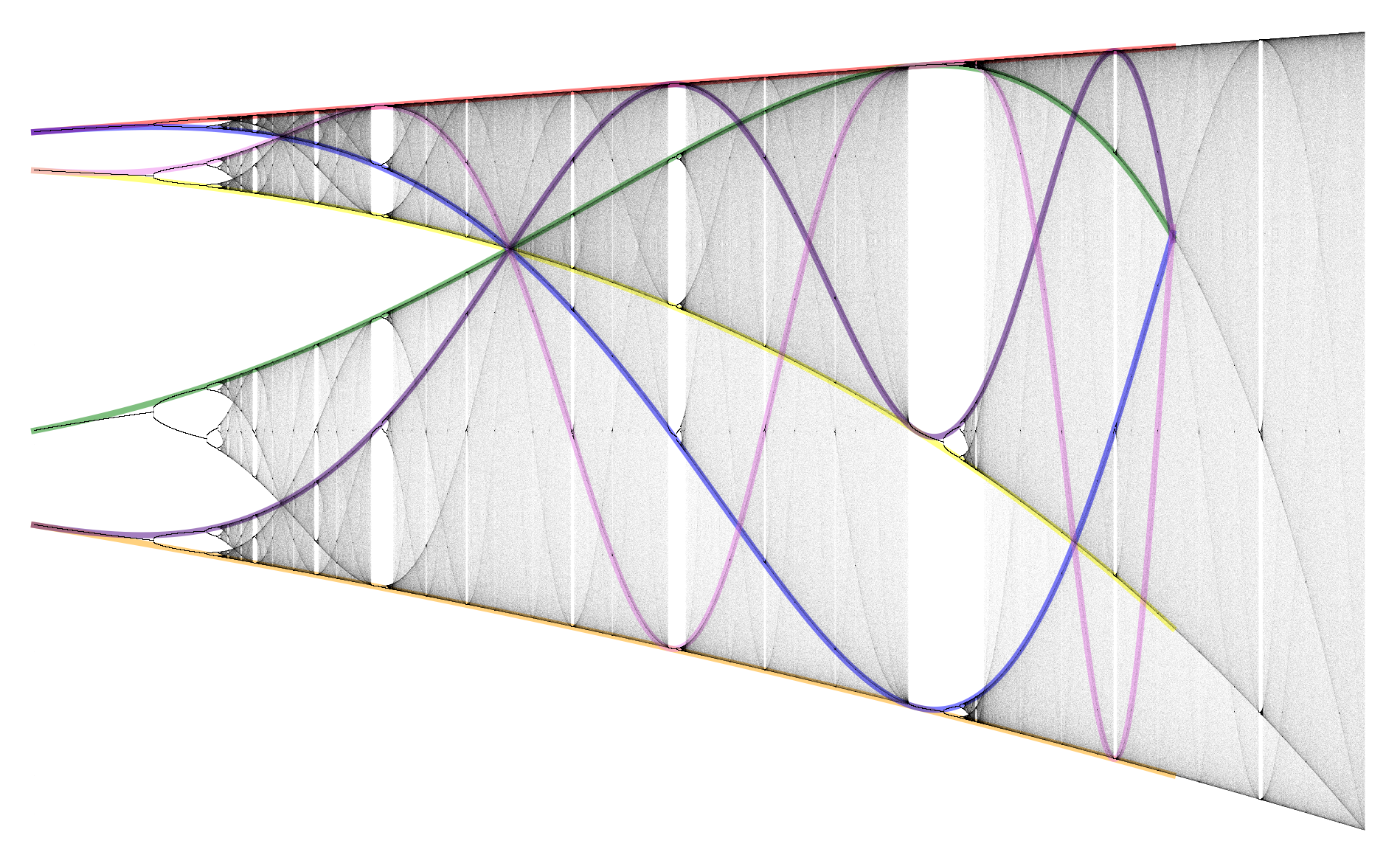
Clifford attractor
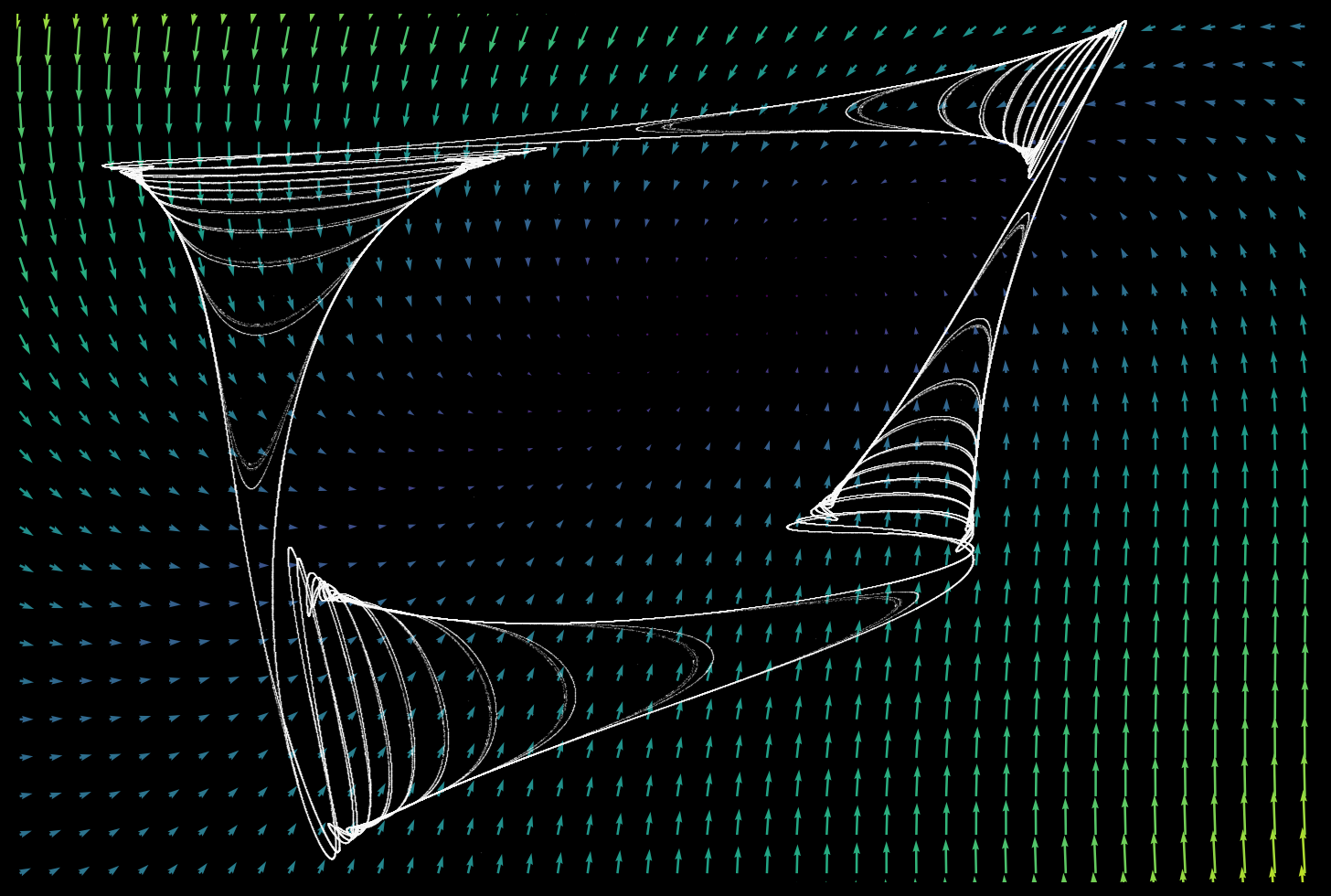
Grid map

Pendulum phase space

Boundaries
Trajectories of any dynamical equation may stay bounded or else diverge towards infinity. The borders between bounded and unbounded trajectories can take on spectacular fractal geometries.
Polynomial roots I

Polynomial roots II

Julia sets

Mandelbrot set

Henon map

Clifford map

Logistic map

Foundations
Primes are unpredictable
\[\lnot \exists n, m : (g_n, g_{n+1}, g_{n+2}, ... , g_{n + m - 1}) \\ = (g_{n+m}, g_{n+m+1}, g_{n+m+2}, ..., g_{n + 2m - 1}) \\ = (g_{n+2m}, g_{n+2m+1}, g_{n+2m+2}, ..., g_{n + 3m - 1}) \\ \; \; \vdots\]Aperiodicity implies sensitivity to initial conditions
\[f(x) : f^n(x(0)) \neq f^{n+k}(x(0)) \forall k \implies \\ \forall x_1, x_2 : \lvert x_1 - x_2 \rvert < \epsilon, \; \\ \exists n \; : \lvert f^n(x_1) - f^n(x_2) \rvert > \epsilon\]Aperiodic maps, irrational numbers, and solvable problems
\[\Bbb R - \Bbb Q \sim \{f(x) : f^n(x(0)) \neq f^k(x(0))\} \\ \text{given} \; n, k \in \Bbb N \; \text{and} \; k \neq n \\\]Irrational numbers on the real line
\[\Bbb R \neq \{ ... x \in \Bbb Q, \; y \in \Bbb I, \; z \in \Bbb Q ... \}\]Discontinuous aperiodic maps
\[\{ f_{continuous} \} \sim \Bbb R \\ \{ f \} \sim 2^{\Bbb R}\]Poincaré-Bendixson and dimension
\[D=2 \implies \\ \forall f\in \{f_c\} \; \exists n, k: f^n(x) = f^k(x) \; if \; n \neq k\]Computability and Periodicity I: the Church-Turing thesis
\[\\ \{i_0 \to O_0, i_1 \to O_1, i_2 \to O_2 ...\}\]Computability and Periodicity II
\[x_{n+1} = 4x_n(1-x_n) \implies \\ x_n = \sin^2(\pi 2^n \theta)\]Nonlinearity and dimension
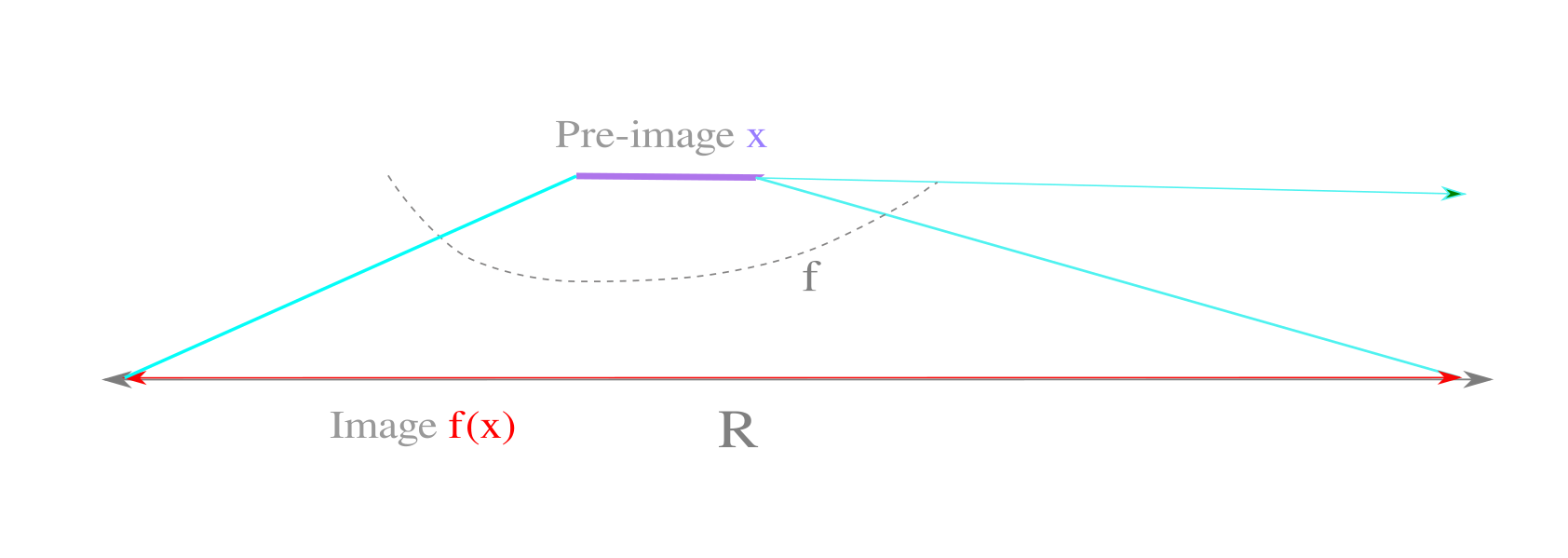
Reversibility and periodicity
\[x_{n+1} = rx_n(1-x_n) \\ \; \\ x_{n} = \frac{r \pm \sqrt{r^2-4rx_{n+1}}}{2r}\]Additive transformations

Fractal Geometry

Physics
As for any natural science, an attempt to explain observations and predict future ones using hypothetical statements called theories. Unlike the case for axiomatic mathematics, such theories are never proven because some future observation may be more accurately accounted for by a different theory. As many different theories can accurately describe or predict any given set of observations, it is customary to favor the simplest as a result of Occam’s razor.
Three Body Problem I
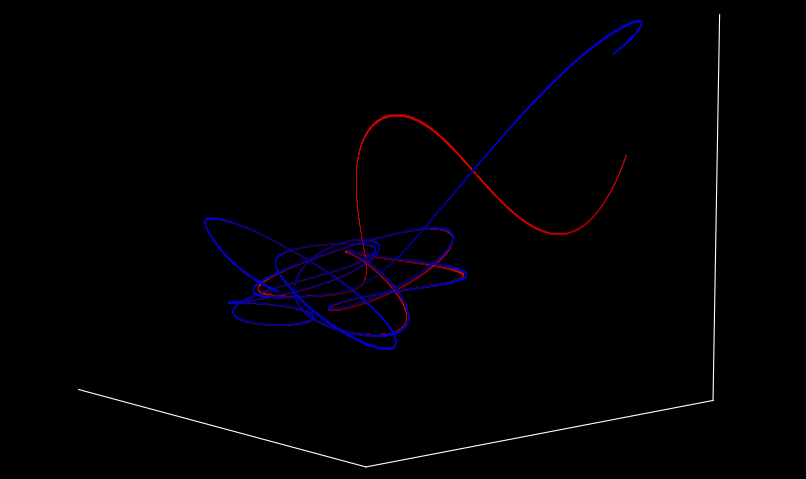
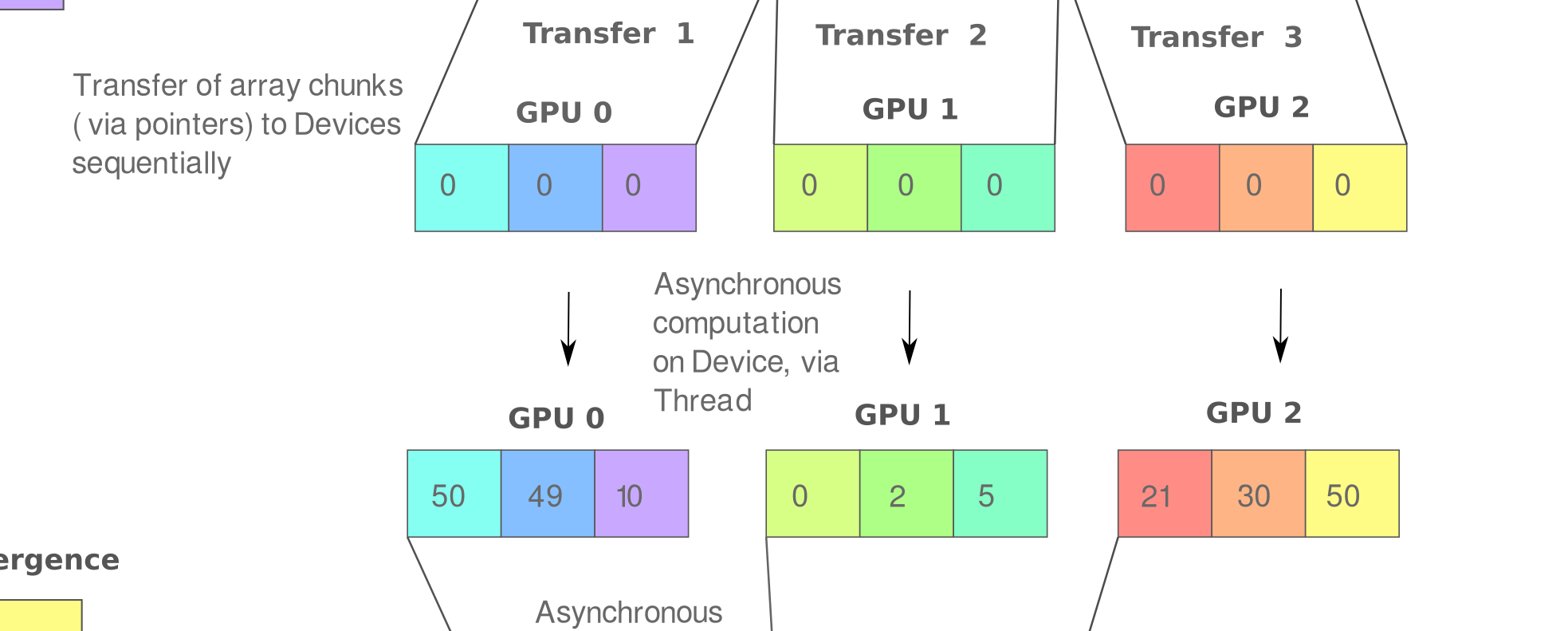
Three Body Problem II: Parallelized Computation with CUDA
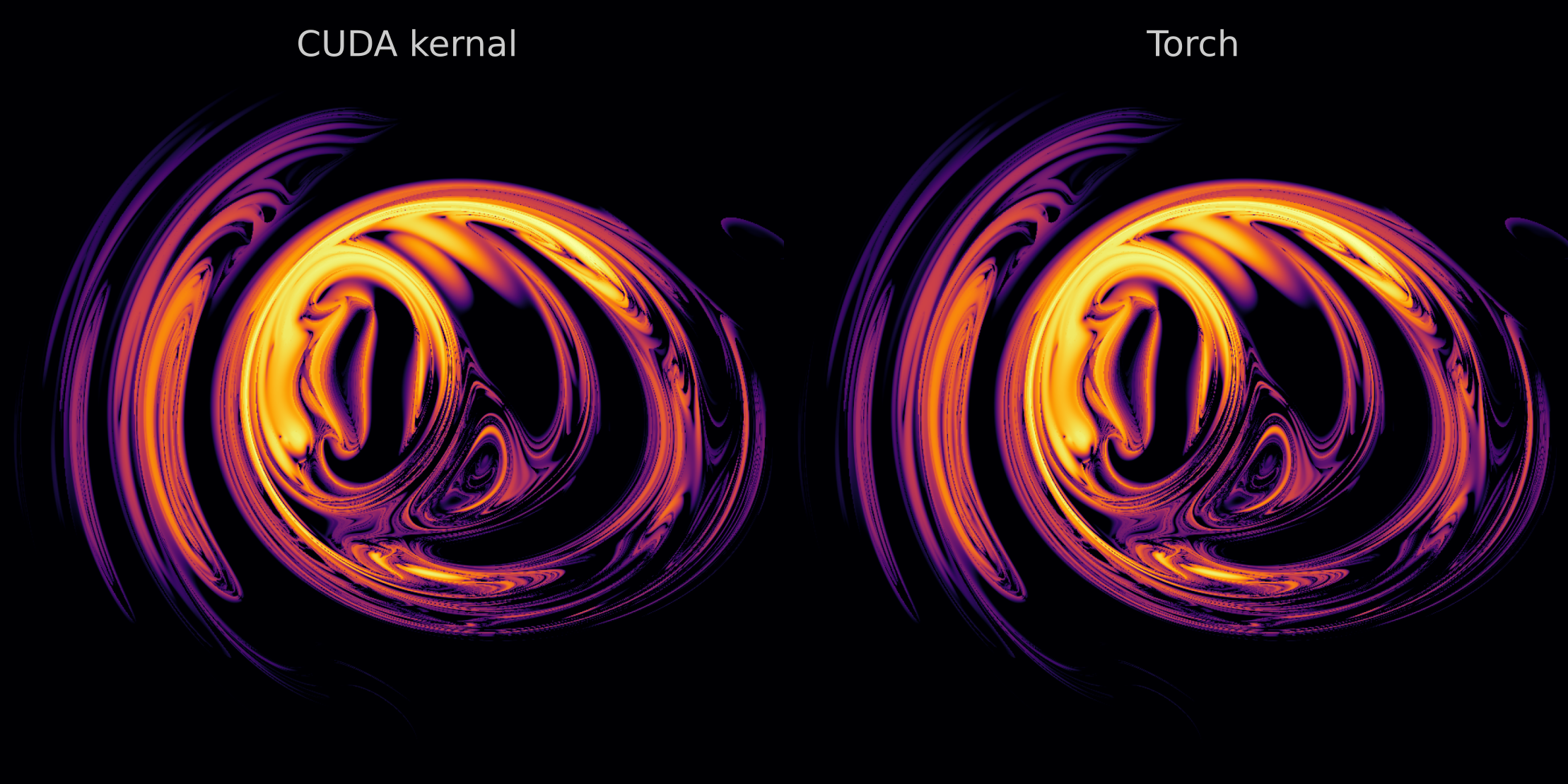
Three Body Problem III: Distributed Multi-GPU simulations
Entropy

Quantum Mechanics
\[P_{12} \neq P_1 + P_2 \\ P_{12} = P_1 + P_2 + 2\sqrt{P_1P_2}cos \delta\]Biology
The study of life, observations of which display many of the features of nonlinear mathematical systems: an attractive state resistant to perturbation, lack of exact repeats, and simple instructions giving rise to intricate shapes and movements.
Genetic Information Problem

Homeostasis

Deep Learning
Machine learning with layered representations. Originally inspired by efforts to model the animalian nervous system, much work today is of somewhat dubious biological relevance but is extraordinarily potent for a wide range of applications. For some of these pages and more as academic papers, see here.
Image Classification
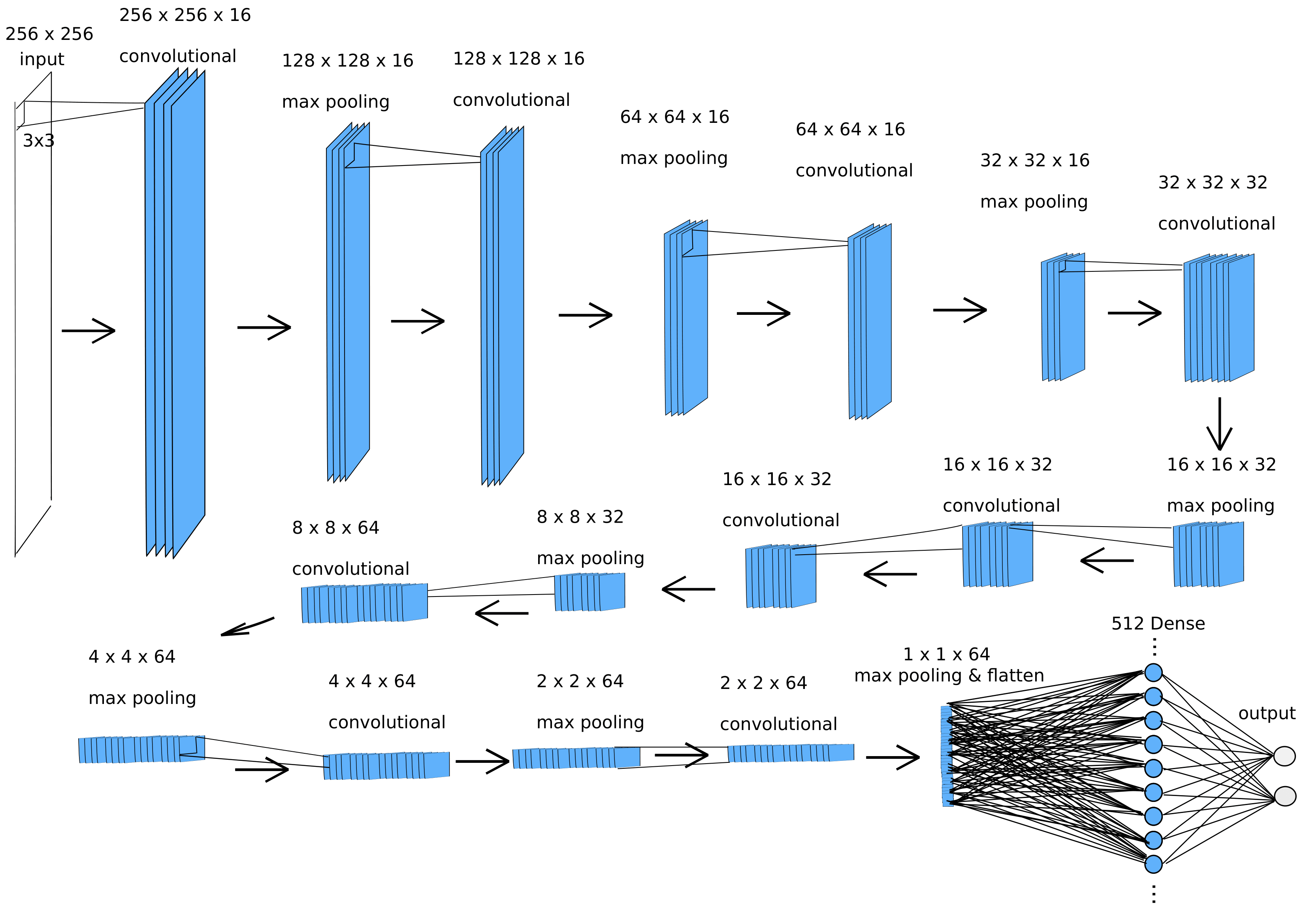
Input Attribution and Adversarial Examples

Input Generation I: Classifiers

Input Generation II: Vectorization and Latent Space Embedding
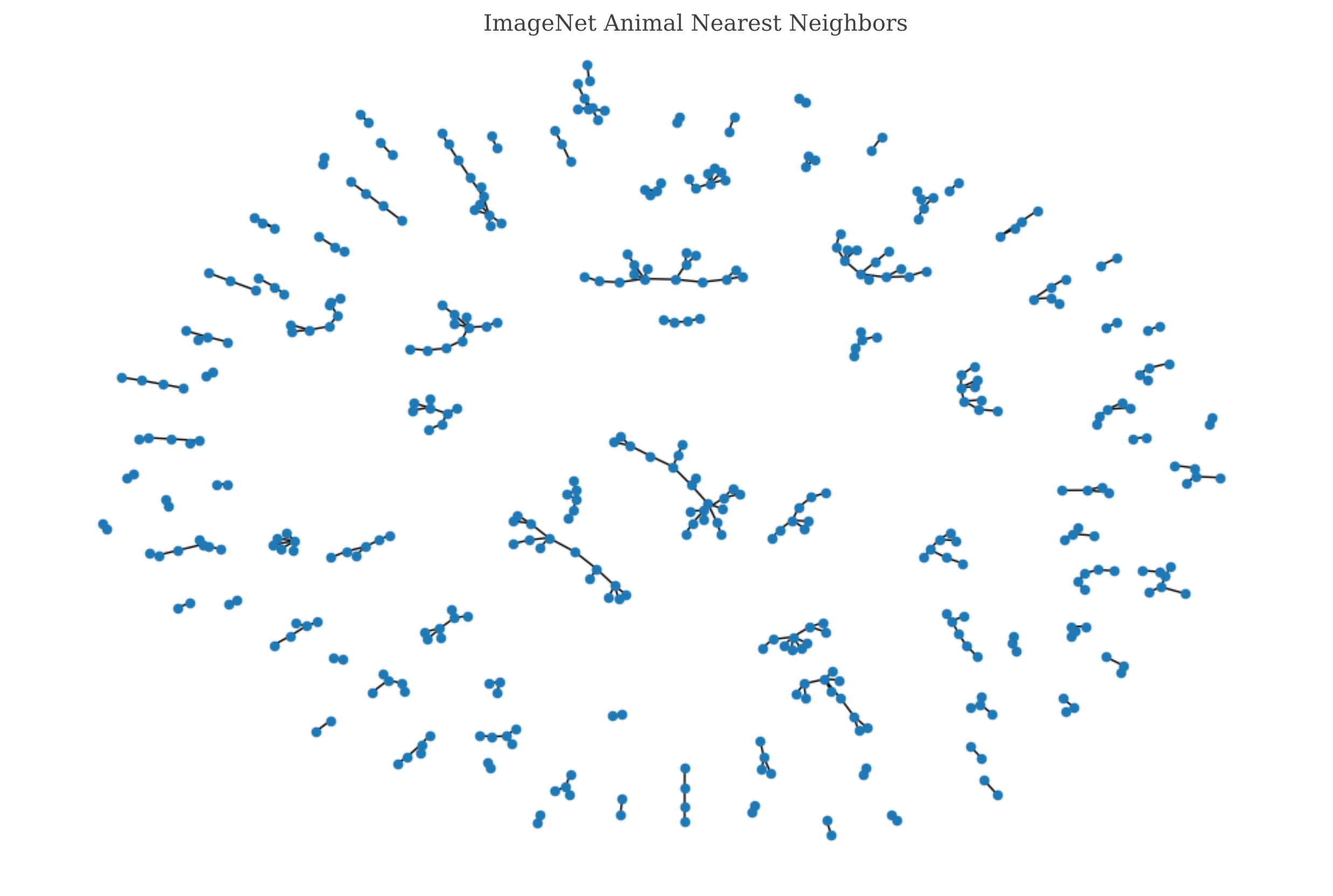
Input Generation III: Input Representations

Input Representation I: Depth and Representation Accuracy

Input Representation II: Vision Transformers

Language Representation I: Spatial Information
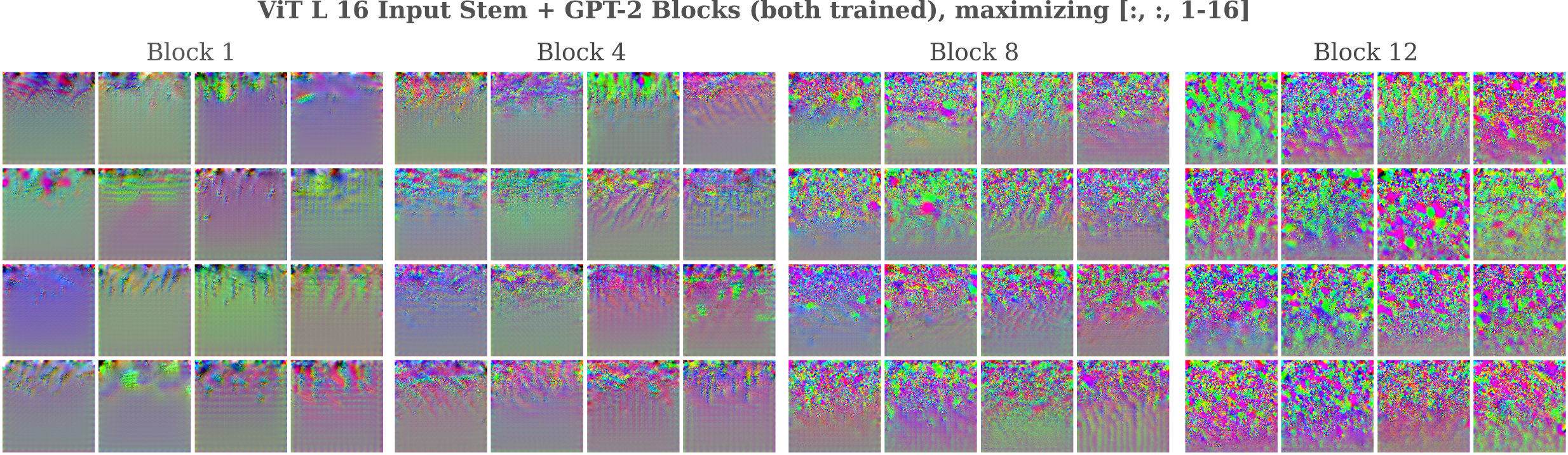
Language Representation II: Sense and Nonsense
\[\mathtt{This \; is \; a \; prompt \; sentence} \\ \mathtt{channelAvailability \; is \; a \; prompt \; sentence} \\ \mathtt{channelAvailability \; millenn \; a \; prompt \; sentence} \\ \dots \\ \mathtt{redessenal \; millenn-+-+DragonMagazine}\]Language Representation III: Noisy Communication on a Discrete Channel
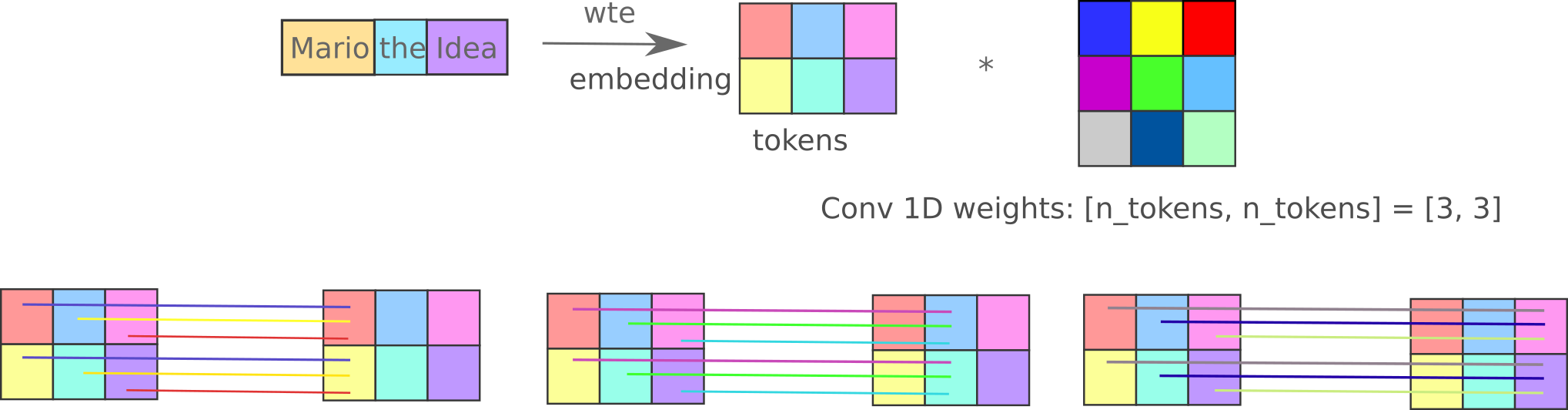
\[a_g([:, :, :2202]) = \mathtt{Mario \; the \; Idea \; versus \; Mario \; the \; Man} \\ a_g([:, :, :2201]) = \mathtt{largerpectedino missionville printed satisfiedward}\]Language Representation IV: Inter-token communication and Masked Mixers
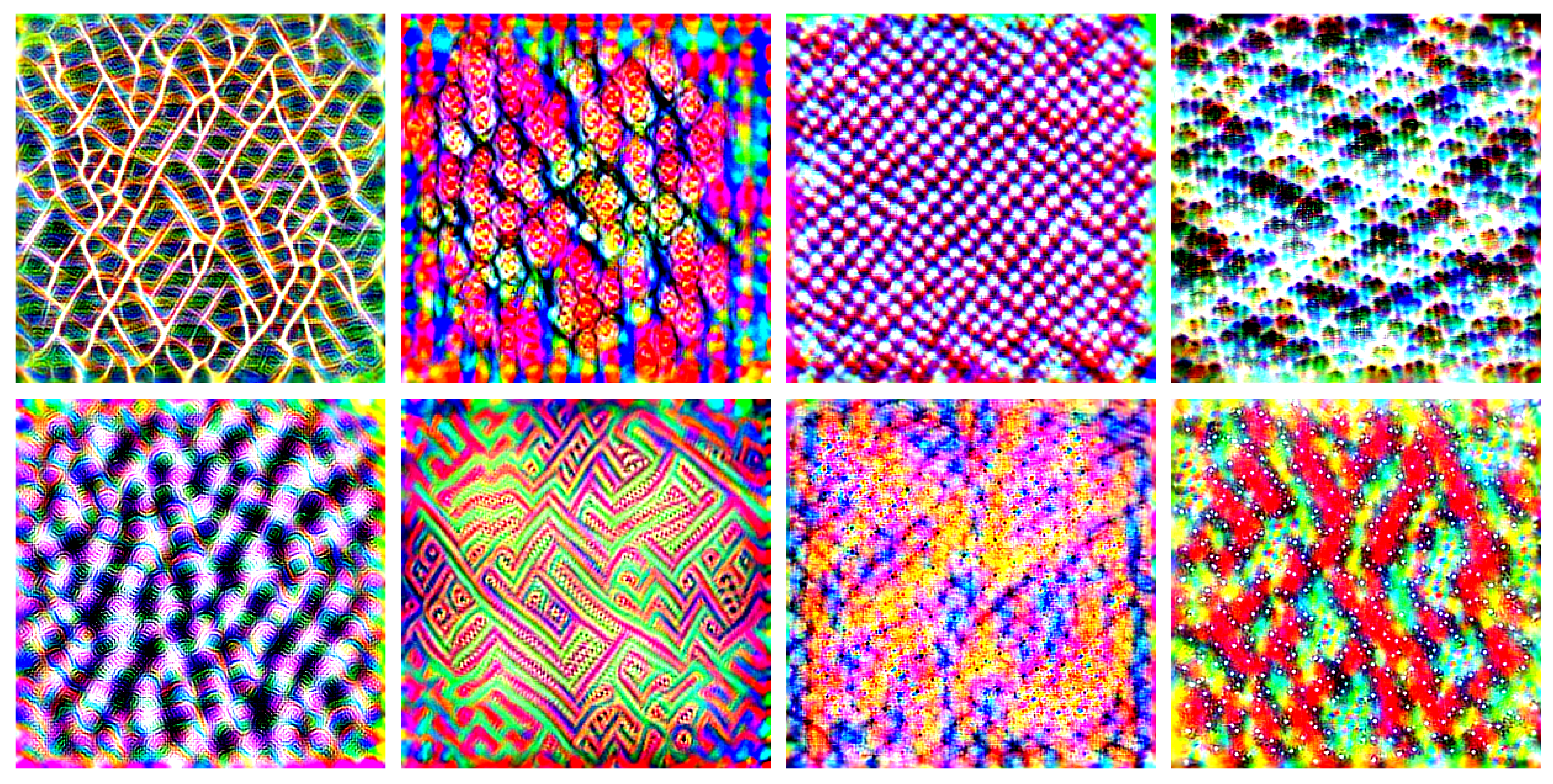
Language Features
\[O_f = [:, \; :, \; 2000-2004] \\ a_g = \mathtt{called \; called \; called \; called \; called} \\ \mathtt{ItemItemItemItemItem} \\ \mathtt{urauraurauraura} \\ \mathtt{vecvecvecvecvec} \\ \mathtt{emeemeemeemeeme} \\\]Feature Visualization I

Feature Visualization II: Deep Dream

Feature Visualization III: Transformers and Mixers
Language Mixers
Language Mixers II: Large datasets, Bidirectional and one-pass modeling, Retrieval

Language Mixers III: Optimization
\[x_{(k+1)} = x_{(k)} - (J(x_{(k)})^{-1}F(x_{(k)}) \\ \; \\ \theta_W = (X^TX)^{-1} X^T y = X^+ y, \\ X^+ = \lim_{\alpha \to 0^+} (X^TX + \alpha I)^{-1} X^T\]Entropy Estimation
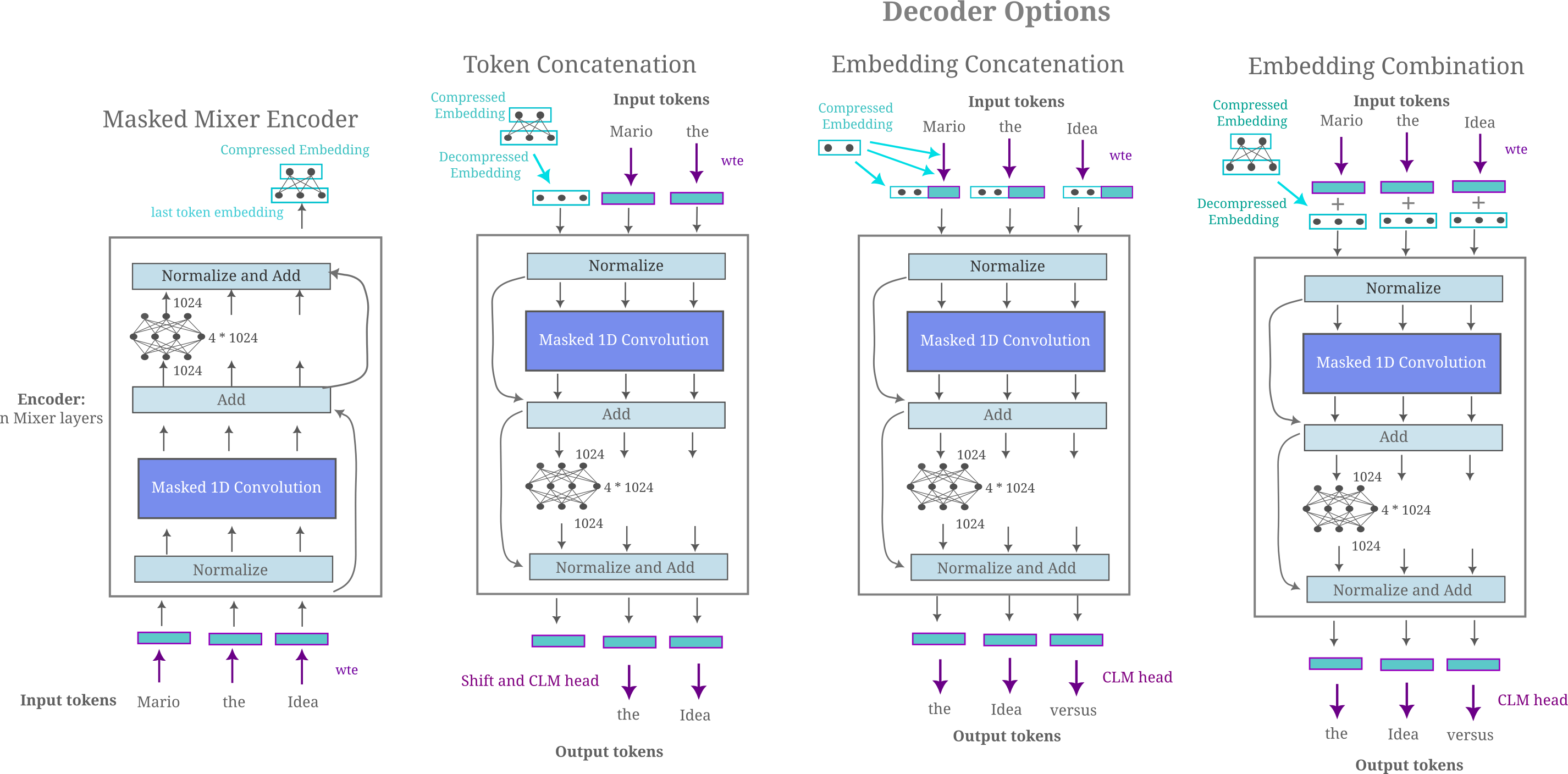
Memory Models
\[I_e = 1 - \frac{H(p, q)}{H(p_0, q)} = 1 - \frac{- \sum_x q(x) \log (p(x))}{- \sum_x q_0(x) \log (p(x))}\]Structured Recurrent Mixers
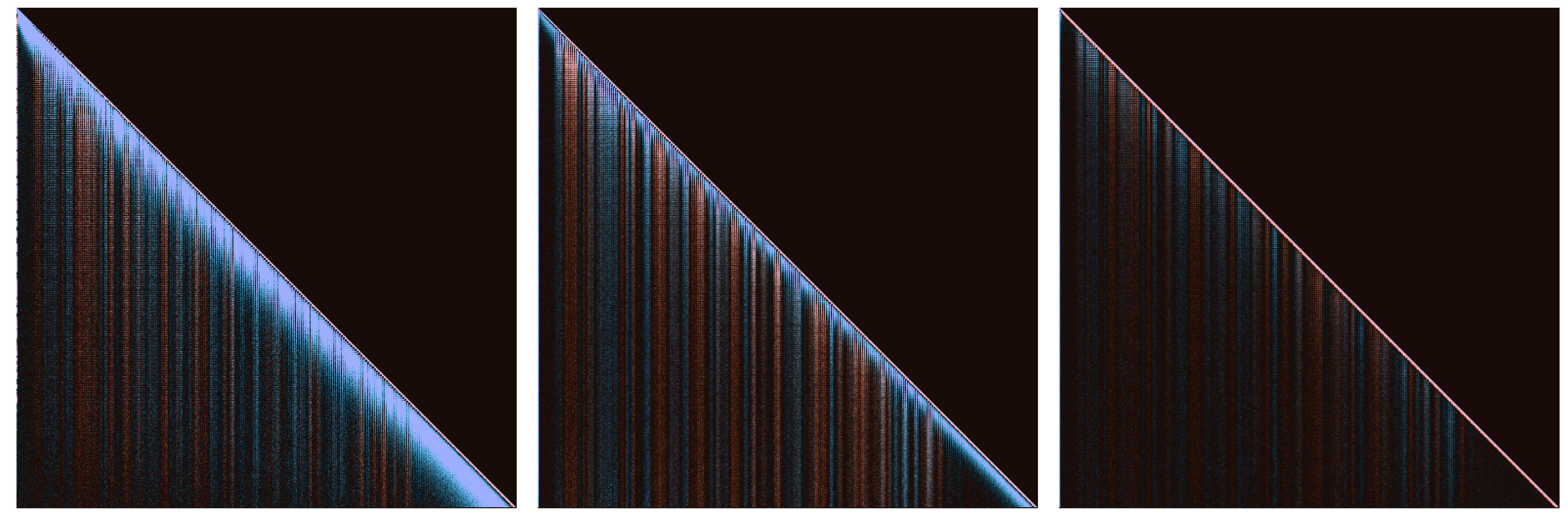
Linear Language Models
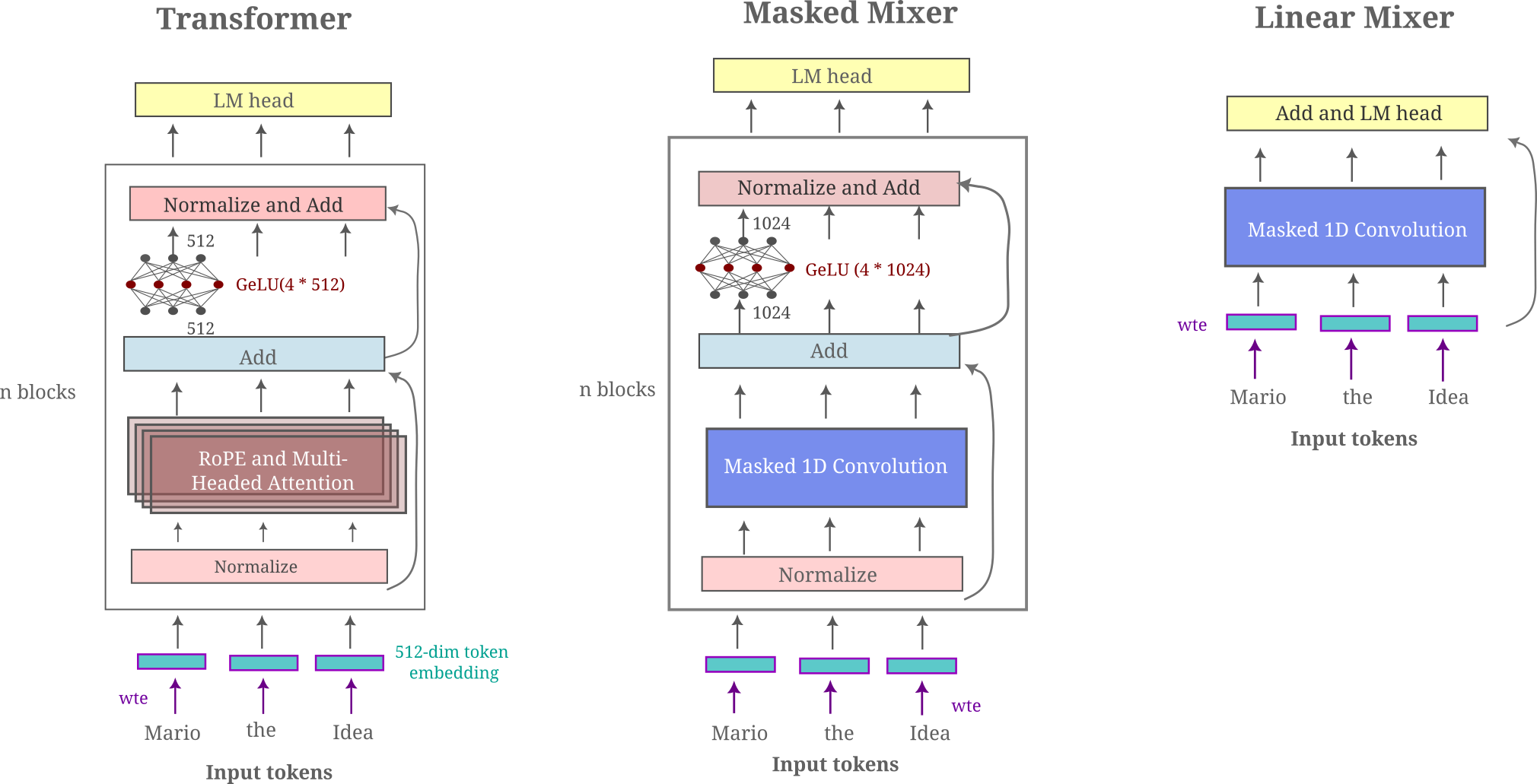
Vision Autoencoders

Diffusion Inversion

Generative Adversarial Networks

Normalization and Gradient Stability
Small Language Models for Abstract Sequences
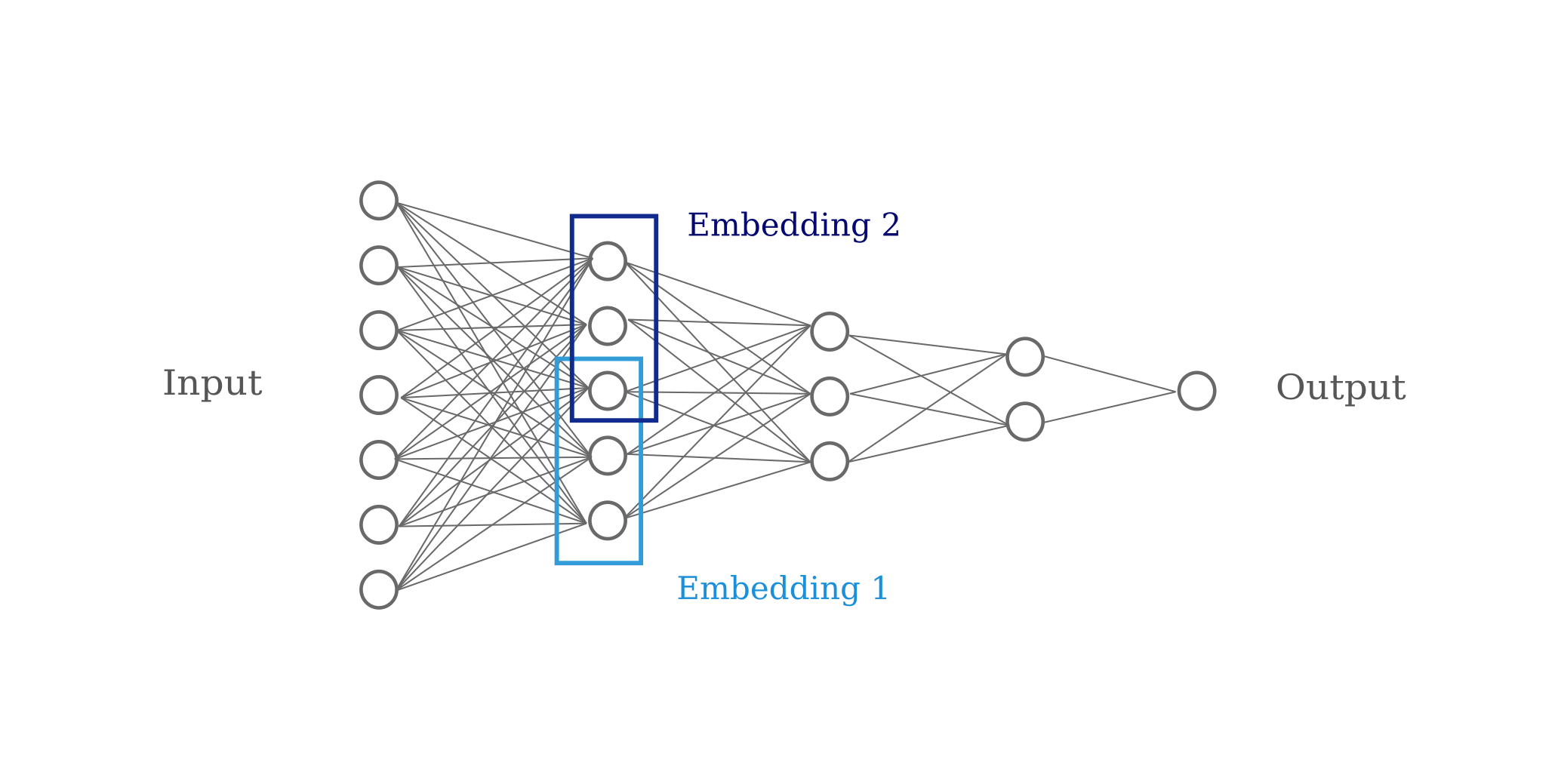
Interpreting Sequence Models
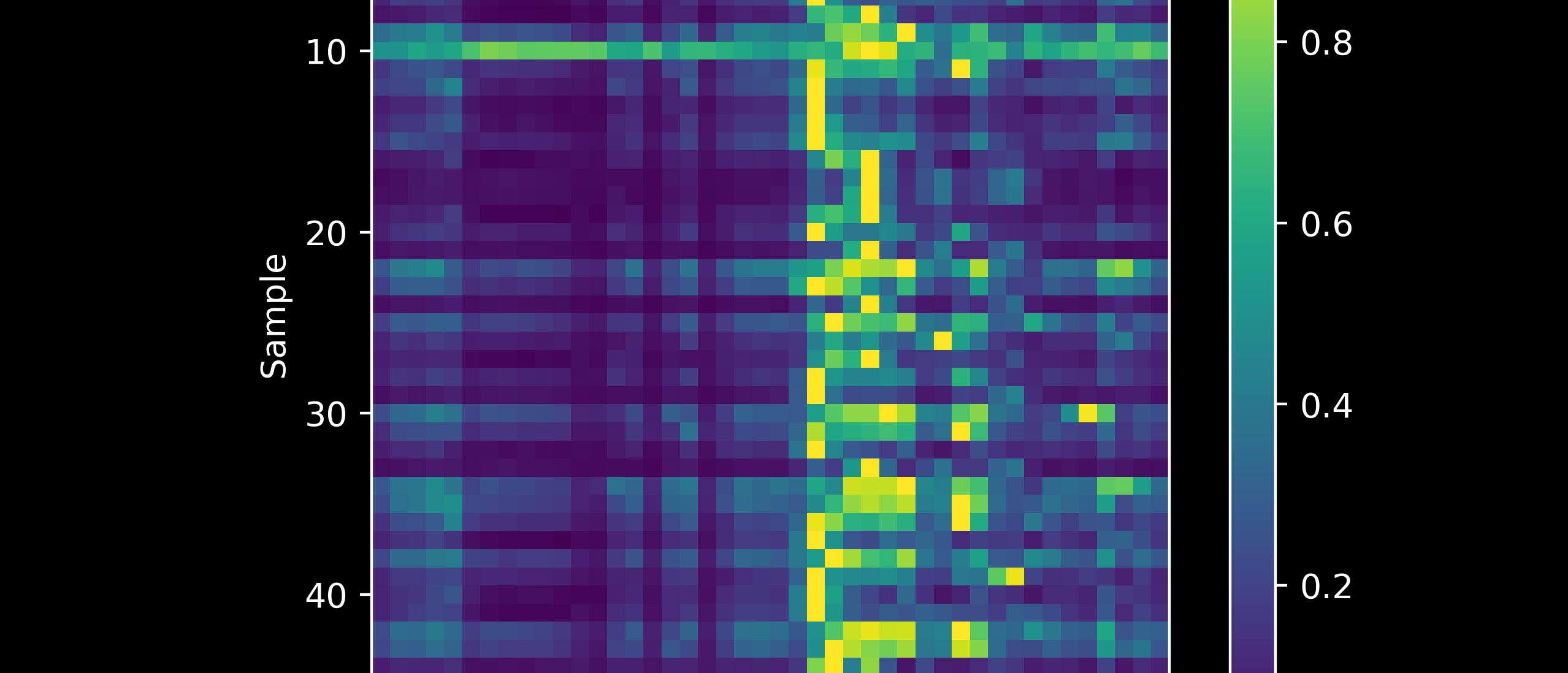
Limitations of Neural Networks
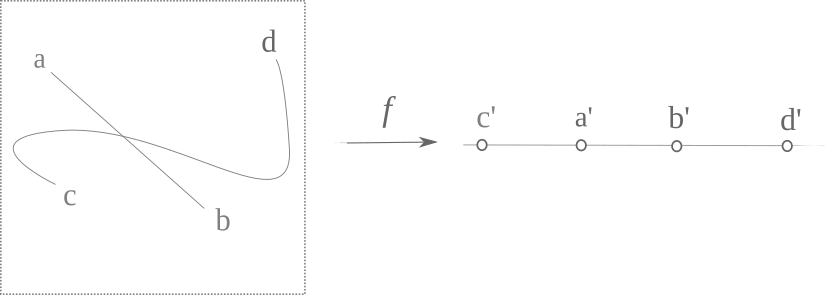
Small Projects
Game puzzles

Programs to compute things
\[\; \\ \begin{vmatrix} a_{00} & a_{01} & a_{02} & \cdots & a_{0n} \\ a_{10} & a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n0} & a_{n1} & a_{n2} & \cdots & a_{nn} \\ \end{vmatrix} \; \\\] \[\; \\ 5!_{10} = 12\mathbf{0} \to 1 \\ 20!_{10} = 243290200817664\mathbf{0000} \to 4 \\ n!_k \to ? \; \\\]Low Voltage
In many ways less stressful than high voltage engineering, still exciting and rewarding.
Deep Learning Server

High Voltage
High voltage engineering projects: follow the links for more on arcs and plasma.
Tesla coil

Fusor
